Auditory signal processing, 음향음성학 기초

최근 소리를 활용한 연구를 진행하고 있는데, 기본적인 음향음성학 및 신호처리에 대한 기본 개념이 약하여 이를 정리하면서 공부하고자 한다.

1. 소리는 무엇인가?

소리란 어떤 음원에서 만들어진 진동이 대기중에 있는 공기분자들을 움직이게 하고 이것이 전달되어 파동을 일으키는 현상이며, 이 때 이 파동을 타고 우리 귀에서 인식하는 것을 "들린다"라고 표현한다. 이와 같이 소리가 만들어 내는 파동을 "음파(Sound Wave)"라고 한다.

음파는 일반적으로 파동의 형태와 같이 단순파와 복잡파로 볼 수 있는데, 단순파는 흔히 말하는 사인함수와 같은 꼴로 일정한 패턴이 반복되는 음파의 가장 단순한 형태이다. 반면에 복잡파는 이러한 단순파들의 합으로 이루어져있으며, 이 분야를 공부하는 사람들이 많이 들어봤을 푸리에 변환의 푸리에가 모든 주기파는 일정한 단순파들의 합이라는 것을 밝혔다. 이는 다시 말하면 어떠한 복잡한 형태의 음파도 단순파로 쪼개서 분석할 수 있다는 것이다.

음파

이 때,
주파수 - 1초 동안 음파의 주기가 반복되는 횟수 (Hz),
주기 - 1/f, 파장, 진폭 등을 관측할 수 있게 된다.
진폭은 다른 관점으로는 공기분자가 진동에 의하여 인접한 공기분자를 미는 힘을 의미하며, 이는 소리에서의 상대적인 강도인 데시벨(db)와 관련이 있다.

2. 스펙트럼이란?

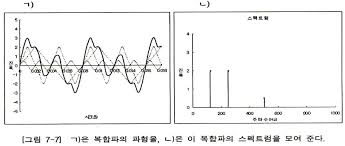
스펙트럼은 음향신호 분석에서 매우 중요한 데, 일반 단순파의 경우 파형 자체만으로 진폭이나 주파수 등을 쉽게 분석할 수 있지만 복잡파의 경우는 그렇지 못하기에, 진폭과 주파수를 축으로 하여 복합파를 분석하여 어떠한 단순파들의 합으로 이루어진 것인지 분석할 수 있게 된다.

스펙트럼

3. 스펙트로그램이란?

음향 신호를 주파수와 진폭으로 나타낸 스펙트럼에서 시간의 차원을 더하여 분석하는 것을 스펙트로그램이라고 한다.

스펙트로그램

3.1 윈도우 길이(Window Length): 분석 대상의 파형의 길이
3.2 주파수 대역폭(band width): 복합파의 분석을 위한 여과기의 폭
- 윈도우의 길이가 길면 주파수의 대역폭은 좁다. vice versa.
- (협역 스펙트로그램) 윈도우의 길이가 길고 주파수 대역폭이 좁다는 것: 짧은 시간 변화에 충분한 정보를 얻을 수 있기에 개별 성분 주파수와 그 진폭에 대한 정보 분석에 용이하다. (가로줄의 가는 선이 관찰)
- (광역 스펙트로그램) 윈도우의 길이가 짧고 주파수 대역폭이 넓다는 것: 어떤 주파수 대역에 에너지가 몰려 있는지 정보를 얻기 쉬워서 음형대(formant)분석에 용이하며 시간 정보 얻기에 용이하나, 개별 주파수 분석이 힘들다는 점이 있다.  (가로로 굵은 띠 관찰)

4. 음압, 강도, 데시벨(dB)

 소리의 진폭은 음압이며, 파형이 전달되는 힘은 강도라 한다.
이 때 소리의 상대적인 강도를 데시벨이라 하며, 흔히 20dB을 조용한 느낌, 60-70dB가 일상적인 발화, 100dB을 고함소리로 인식한다.

5. 디지털 신호처리

음성과 같은 아날로그 신호를 디지털 신호로 바꾸는 과정을 표본화(Sampling)이라 하며, 1초당 몇개의 점을 선택하여 원 신호의 정보를 저장할 지 결정하는 것을 sampling rate을 정한다고 한다. 결론부터 얘기하자면, 표본추출률은 우리가 관심을 두고자 하는 최대 주파수 값의 2배가 되도록 하여야 한다.(Nyquist's sampling theory: 적절한 표본추출률은 아날로그 시그널과 동일한 정보를 갖게 한다.)

표본추출률(sampling rate)가 주파수 관련 정보를 얻는 과정인 반면, 진폭에 관련된 정보를 저장하는 것을 결정하는 것을 양자화(quantization)이라 한다. 단위는 비트로, 일반적으로 사람의 목소리는 12비트(2^12) 음악CD는 16비트 변환을 하게 되며, 너무 낮으면 quantization noise가 발생할 수 있다.

 

다음장에서는 Fourier Transform에 대해서...